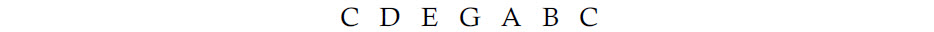You Are Reading the First 6 FREE Chapters (470 pages)
3 to 2 Ratio: The Basis of Pythagorean Tuning
The next step is to play all six notes, all derived from the 3 to 2 ratio, in the same octave, and in scale order. Then add another C to complete the scale. Now you have the following seven-note scale:

There you go. With only the 3 to 2 ratio, the basis of Pythagorean tuing, that’s almost the diatonic major scale.
You can construct a good many of the world’s popular musical scales simply by using notes derived from consecutive frequency jumps in the ratio of 3:2, the ratio of the perfect fifth interval.
And, as discussed earlier, when you plunk a bunch of these notes into the same octave, you end up with other simple frequency ratios within the scale as well, such as 2:1 (octave), 4:3 (perfect fourth), 5:4 (major third), and so on.
So, since Mr. Pythagor figured out the principle of creating scales derived from simple frequency ratios, such scales are called Pythagorean scales. The “do-re-mi” major diatonic scale is a Pythagorean scale, even though it’s not perfectly based on consecutive intervals in ratios of 3:2.
“Not perfectly” means something goes awry. Here’s how:
So far, you’ve seen that if you use the strict Pythagorean method, you get these six different notes (the octave note is repeated):